In the previous article, we explored the intuitions behind feedforward propagation in an Artificial Neural Network(ANN). We know how activation function is applied to the equation of a straight line and how it squashes the value of a function between its lower and upper bound. Furthermore, this idea of applying activation function is extended to all the neurons associated with the learning in ANN. In this article, we will explore the notion behind the backpropagation algorithm.

Intuitions Behind Backpropagation

Imagine that our first feedforward propagation gives us an output at the output layer. It is very obvious that the output as predicted in the very first attempt of forward propagation is not going to match our actual output. We call this mismatch between the predicted output and the actual output as the error or loss function. Our main goal is to minimize this error or loss function until the predicted output falls in the proximity of the accepted threshold of actual output.

To gain intuitions behind the backpropagation, let us imagine playing a game of chess against a very powerful Chess Engine. Let’s assume we’re provided with ‘undo’ move functionality in the game so that we’re allowed to undo our move and try a new move, to come up with a better move. Let’s assume, we’ve lost our first game against the engine. Now, we want to analyze the same game and want to try different moves and combinations in order to come up with better performance. We would undo the last move i.e., the one where we lose the game and analyze the position. After a few possible take backs along with the combination of new moves, we would have improved our training & performance.

The important thing to note here is we started the game by moving forward with our best moves, and reaching the last move and then started propagating backward in steps from the last move to the first move. The feedforward propagation along with backpropagation constitute the training of our ANN. ANN starts with the random guess of weights and biases to predict the output (feedforward propagation) and then, it back propagates the predicted output across each layer of ANN to minimize the loss function (backpropagation).

The ANN is also referred to as a layered learning architecture as it undergoes multiple forward propagation and backward propagation simultaneously (in an iteration) across the layers in a sequence.

Theory of Backpropagation

The backpropagation follows the feedforward propagation in a loop until there exists the permissible error between the desired output & an actual output.

• The backpropagation aims to minimize the cost function by adjusting the network's weights and biases.
• The level of adjustment is determined by the gradients of the cost function with respect to those parameters (both weights and biases).
• The gradient determines how much a parameter needs to change (in the positive or negative direction) to minimize loss/cost function.
• The computation of gradient is done on the basis of the chain rule in calculus.

Concept of Partial Derivatives & Chain Rule:

Consider two variables ‘y’ and ‘x’. Assume ‘y’ is related to ‘x’ by some function as: y = f(x)

However, the variable ‘x’ is related to another variable ‘z’ by some other function as: x = g(z)

We’re interested in knowing how a change in variable ‘z’ affects the variable ‘y.’ It can be calculated from the simple intuition as:

Change in y due to change in z = (Change in x due to change in z ) * (Change in y due to change in x )

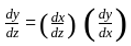
On rearranging the terms we get:

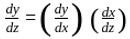
NOTE: The change in ‘f’ is dependent on a single variable ‘x’, so we use the total derivative to denote the change in ‘f’ with respect to ‘x’ i.e y = f(x). In case, if a change in ‘f’ is dependent on two or more variables like c = f(x,y), then we use partial derivatives to denote the change in ‘f’ with respect to ‘x’ and ‘y .’ This is the concept of the chain rule and partial derivatives which is applicable to our ANN in an exact manner, which is discussed in the next section.

Feedforward & Backward Prop in Action

Terminology:

• x: input feature associated with the input layer of ANN
• w : weights associated with the layers of ANN
• b : bias associated with the layers of ANN
• z : function of a linear combination of weight & bias
• a : activation function as applied to ‘z’
• yhat: predicted output
• y : actual output
• L: Loss Function as modeled in terms of predicted output & actual output
• dw : derivative of loss function w.r.t weight
• db : derivative of loss function w.r.t bias
• da: derivative of loss function w.r.t output of an activation function

Consider fig1 to look at the microscopic details of what’s happening inside the ANN. For simplicity, we are assuming a partial structure of ANN to visualize how backpropagation is working in conjunction with feedforward propagation.

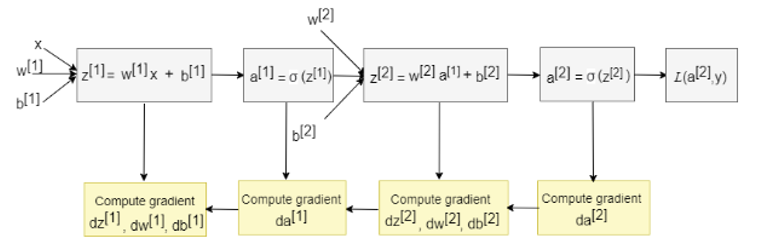
Forward Propagation

• ANN starts with initial random guesses of weight, and bias at the input layer and then calculates the parameter z , for corresponding w and b.

• Next, the activation function (sigmoid, in the above example) is applied to z.

• The above steps are repetitive in nature until we reach the last output layer. It is to be noted that, the output of the first layer serves as an input of the second layer, and again the output of the second layer serves as an input of the third layer and so on.

• At the last output layer, we have our predicted output (yhat) and this would differ from our actual output (y). We model our loss function in terms of predicted output, available as a[2]and the actual output known to us as y.

Backpropagation

• For our ANN, da can be defined as:

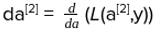
• Next, we can calculate dz using the chain rule as:

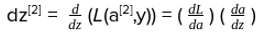
• The gradient of weight & bias can be calculated as:

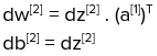
• Similarly, backpropagation calculates all the gradients of weights and biases associated with each layer with the goal of minimizing the error in an iterative way.

It is beyond the scope of this article to include the derivation of the above formulae of backpropagation, as it requires complex derivative calculations. However, when you’re coding a neural network using Tensorflow or any other framework, you don’t need to remember any mathematical formulae as it will be explicitly taken care of by the library itself.

Epoch Vs Batch size Vs Iteration

Epoch: It is referred to as one cycle through the full training dataset. One epoch can be thought of as one forward pass and one backward pass of all the training examples.

Batch-size: Often the training set itself is larger, so we divide our entire dataset into a number of batches. Batch-size refers to the number of training examples in one forward/backward pass. Batch-size is one of the hyper-parameters and is generally decided on the basis of the optimization algorithm employed in the ANN.

Iteration: It is referred to as the number of batches or steps through partitioned packets of the training data, needed to complete one epoch.

For example, if you have 10000 training examples, and your batch size is 5000, then it will take 2 iterations to complete 1 epoch.

NOTE: Epoch is one of the hyperparameters of ANN. It means the user can choose and play around with the value of epochs. One should not choose fewer epochs such that the model is poorly trained and also one should not select a very high number of epochs that our model starts overfitting and give a poor performance on the unseen data.

Conclusion

We have visualized how ANN iterates in a loop of forward & backward propagation in order to minimize the error between the predicted output & the actual output. What we have not covered in this article is the concept of Gradient Descent Algorithm or other optimization algorithms that are used for minimizing the loss function. However, in the next article, I will try to cover the in-depth intuitions & visualization behind optimizing the loss function in ANN.

References:

1. Backpropagation

2. What is Backpropagation

3. Neural networks